Data clustering
What is SALR particle clustering?
Data clustering
Is there structure to the data?
Is the data made from distinct/overlapping groups?
These are often the first questions asked when analyzing data, and data clustering helps to answer them by searching for regions in the data where a measure of the difference between the points in each group is minimized. An example of data clustering is shown in this image, where the center of seven different data clusters have been found. Each data points can then be assigned to the cluster that has the smallest difference with itself.
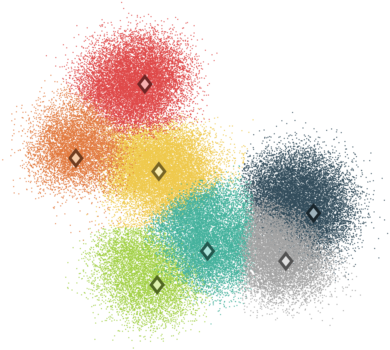
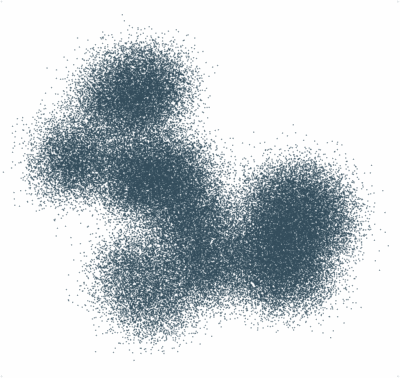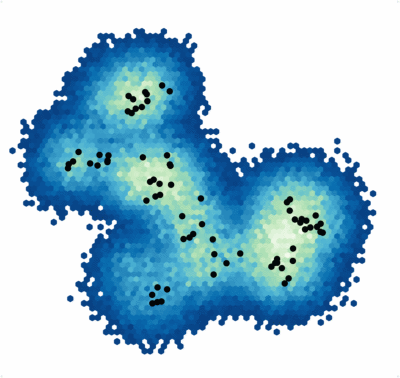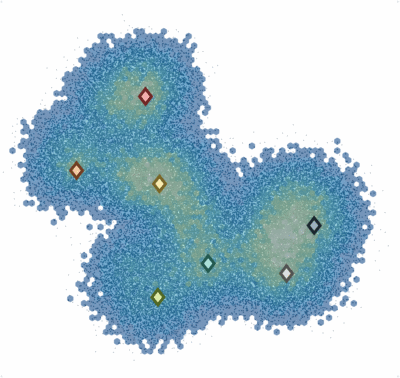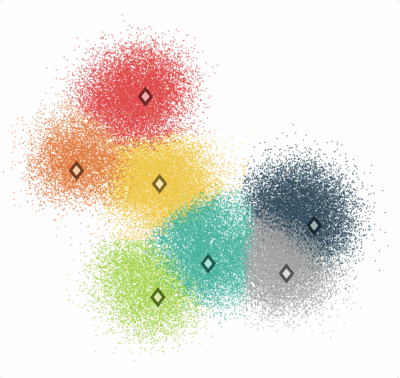
SALR particle clustering
SALR particle clustering locates cluster centers by first creating an intermediate surface
called the »confining potential«. The confining potential can be thought of as being like hills and valleys, with valleys near the locations we think the data clusters could be and hills near the locations where they could not be. The data clusters are then determined by modeling how a set of particles move in the confining potential and extracting the final positions of the particles. The key aspect of SALR clustering is the short-range attractive long-range repulsive interaction of the particles.
Why short-range attractive long-range repulsive interaction?
Consider a set of repulsive particles (e.g. electrons) confined to a region. These particles will try to move as far apart from each other as possible. Image a shows this for 10 particles confined to a region with one valley. If the region the particles are confined to has several valleys, then the particles will try to be near these valleys. Assuming our goal is to have particles at each valley and nowhere else, we must use the same number of particles as valleys (since two particles cannot be near each other), see images b and c. This is a problem as the number of valleys is normally not known before hand, but it can be solved by modifying how the particles interact with each other, so particles near each other are attracted to each other (not repulsed). Now, we can use (many) more particles than we expect to be valleys, and we can have a cluster of particles located at each valley, see image d.

What are the advantages of SALR clustering?
There are three primary advantages of using SALR clustering over other clustering/seed-point detection methods.
- The number of clusters does not need to be known or guessed beforehand, only the approximate size of the clusters must be known.
- The cluster locations are not strongly biased to regions with very high data density, this makes it useful in cases with rare clusters (low density clusters next to high density clusters).
- The cluster locations do not need to have local maximum in the data density, as opposed to mean-shift clustering1, for example.
- SALR clustering can be very fast: one repetition on a 5D data set with 2.7 million points only takes about 2 seconds, as opposed to k-means clustering2 where one repetition takes about 15 seconds.3
- SALR clustering achieves an F1 score that is 8.1% higher than any other method when used for locating the centers of overlapping nuclei, and SALR clustering is able to better locate rare clusters without density maxima than k-means clustering.3
SALR clustering can represent a significant improvement in locating the centers of overlapping convex objects: it locates the correct number of nuclei more often and the nuclei centers more accurately than standard and leading methods; it can significantly improve the performance of previous methods; and it is able to determine, not only the number of clusters, but the correct position of the cluster centers in data clustering while not required a cluster to have a local density maximum. J. Kapaldo et al., (submitted)3
D. Comaniciu and P. Meer, IEEE Transactions on Pattern Analysis and Machine Intelligence 24, 603 (2002). ↩
J. MacQueen, Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability 1, 281 (1967). ↩
J. Kapaldo, X. Han, and D. Mary, (submitted) ↩ ↩2 ↩3
