5D scatter-point data

Load data

dat = load('exampleData\damage_data_5D.mat');
dat = dat.dat;

% Scale by stddev
dat_std = std(dat);
dat = dat./dat_std;

Compute data density

In this step the data is discretized to a grid (binned). The data is initially binned so that the grid completely covers the data range. Using this information the grid range is limited so that the bins have at least density_threshold points. The data is then re-binned using this limited data range and smoothed with a slowish, but memory efficient Gaussian filter. The grid is set to have approximately nbins along each dimension. The actual number of bins will be chosen so that the grid has the same aspect ratio as the data.

nbins = 30;
density_threshold = 20;
smooth_data = true; % Gaussian filter: sigma=0.5, kernal_size=3

[n, cents, sz, data_limits] = binData(dat, nbins, density_threshold, smooth_data, true);

Explore/Visualize the data

Plot isosurfaces of the data density (count). Since the data is 5D, it must be projected down to 3D. Here, dimensions 1, 3, and 4 will be show. Note that the data is very dense in the middle and there are three low density regions extending outwards (and one very low density region).

dimensions = [1,3,4];
isoLevels = [20,150,500,2000];
tick_spacing = 2*ones(1,5);

cmap = brewermap(9,'GnBu');
cmap(1:2,:) = [];

fig = isosurfaceProjectionPlot(n, dimensions, isoLevels,...
    'ColorScale',@(x) x.^(1/2), ...
    'Bin_Centers', cents, ...
    'Tick_Spacing', tick_spacing, ...
    'ColorMap',cmap);

view([50,35])

Setup SALR clustering parameters

The parameters needed to run SALR clustering can all be accessed and set using the class seedPointOptions. This class handles parameter validation as well as computing/visualizing the SALR particle interaction parameters/potential.

options = seedPointOptions();

Set the particle initialization parameters.

• Use a uniform random point distribution. This will overlay a hyper-cubic lattice across the grid with each lattice cell having a volume equal to the volume of a hyper-sphere with radius Wigner_Seitz_Radius. From each lattice cell, a point is then randomly selected from the grid where the confining potential is between Minimum_Initial_Potential and Maximum_Initial_Potential.

options.Point_Selection_Method = 'uniformRandom';
options.Wigner_Seitz_Radius = 5;
options.Wigner_Seitz_Radius_Space = 'grid';
options.Maximum_Initial_Potential = 1/4;
options.Minimum_Initial_Potential = 1/6;

Set confining potential parameters.

• Use a confining potential based on the data density, and scale the confining force to be 0.4 at its 90% value.

options.Potential_Type = 'density';
options.Max_Potential_Force = 0.4;
options.Potential_Padding_Size = 0;
options.Maximum_Memory = 2; % Allow 2 GB for potential gradients per worker.

Set the particle interaction parameter values.

• Note the Potential_Parameters are given in data units.
• The attractive extent in the solver space is 12. Try changing this value; if you decrease the value to about 10, you should see that the resulting seed-points are farther apart from each other and closer to the boundaries of the data. If you increase the value to about 15 you can see that the seed-points get closer to each and farther from the data boundaries.
• Use a Minkowski distance with an exponent of 4. This will help require that the particles are close to each other in all dimensions.

options.Solver_Space_Attractive_Extent = 12;
options.Potential_Parameters = [-1, 0.15*2, 2];
options.Distance_Metric = {'min',4}; % Minkowski distance with exponent 4

Set up replicates and minimum cluster size.

• Here we use 5 replicates and we keep any seed-point that at least 3 of the replicates produce.

options.Iterations = 5;
options.Minimum_Cluster_Size = 3;

Set parameters controlling execution.

• Verbose will output information on the current iteration and the expected time of completion.
• Debug will return extra information.
• Use_Parallel will determine if the iterations are run in parallel. Note each worker will need its own copy of the data. So, a computer with 4 cores needs 4 times as much memory. Unless you are running many iterations, it is likely faster to not use parallel computation due to overhead.

options.Verbose = true;
options.Debug = true;
options.Use_Parallel = false;

Compute seed points

The seed-points are simply computed by passing the binned data, the seedPointOptions, and the data limits.

rng('shuffle') % Ensure in random state
[seedPoints,Info] = computeObjectSeedPoints(n, options, 'data_limits', data_limits);

Plot the results

Plot the the final seed-points as large red dots and the seed-points from each repetition as small black dots. This can be done by creating the markers structure below and passing it to the isosurfaceProjectionPlot function. It is also nice to project the seed-points onto the three axis planes; this can be done by setting a project field in the markers structure to true.

• Note: The seed-points returned by computeObjectSeedPoints are in data units. In order to plot them, we need to convert them back into grid units.

dimensions = [1,3,4];
isoLevels = [20,150,500,2000];
markers = [];

% Helper function to convert the seed points into grid space
data_to_grid = @(t) Info.problem_scales.data_to_grid(t) - ...
    options.Potential_Padding_Size;

lineSpec = @(col,ls,m,ms) struct('Color', col, ...
    'LineStyle', ls, 'Marker', m, 'MarkerSize', ms);

markers(3).dat = data_to_grid(seedPoints);
markers(3).options = lineSpec('r','none','.',15);
markers(3).project = true;

markers(1).dat = data_to_grid(Info.seedPoints_n);
markers(1).options = lineSpec('k','none','.',4);
markers(1).project = true;

isosurfaceProjectionPlot(n, dimensions, isoLevels,...
    'ColorScale',@(x) x.^(1/2), ...
    'Markers', markers, ...
    'Bin_Centers', cents, ...
    'Tick_Spacing', tick_spacing, ...
    'ColorMap',cmap);

view([50,35])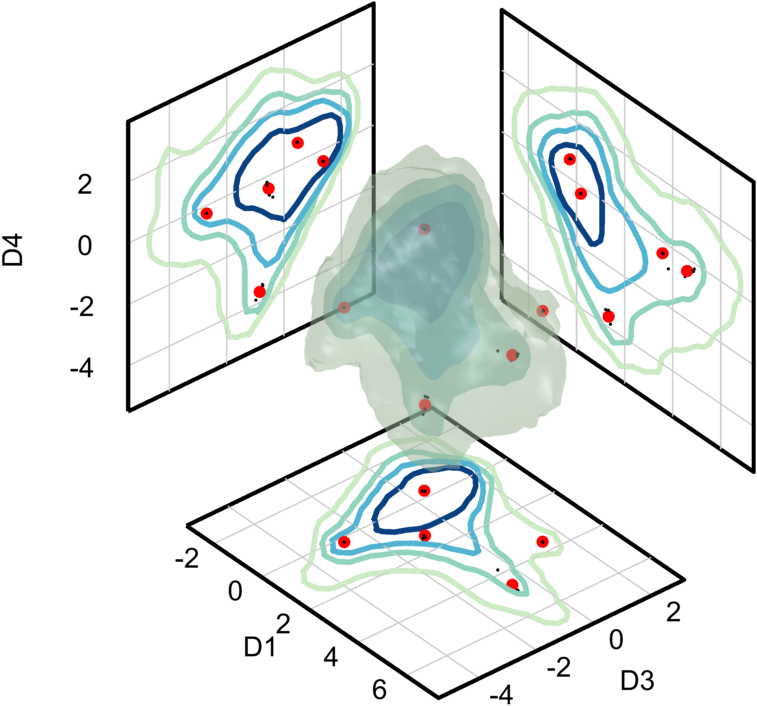

Locate seed-points with k-means

Let’s compare the SALR clustering results to k-means. Use K=4 (since we would not expect the very small low-density point to be found) with 2 replicates, and then plot the results as large blue dots with the SALR clustering results.

K = 4;
kmeans_options = [];
kmeans_options.MaxIter = 200;
kmeans_options.UseParallel = false;

[~,c] = kmeans(dat,K,'Start','plus',...
                        'Options',kmeans_options,...
                        'Replicates',2);

% Plot the results and compare with SALR particle clustering
markers(2).dat = data_to_grid(c);
markers(2).options = lineSpec('b','none','.',15);
markers(2).project = true;

isosurfaceProjectionPlot(n, dimensions, isoLevels,...
    'ColorScale',@(x) x.^(1/2), ...
    'Markers', markers, ...
    'Bin_Centers', cents, ...
    'Tick_Spacing', tick_spacing, ...
    'ColorMap',cmap);

view([50,35])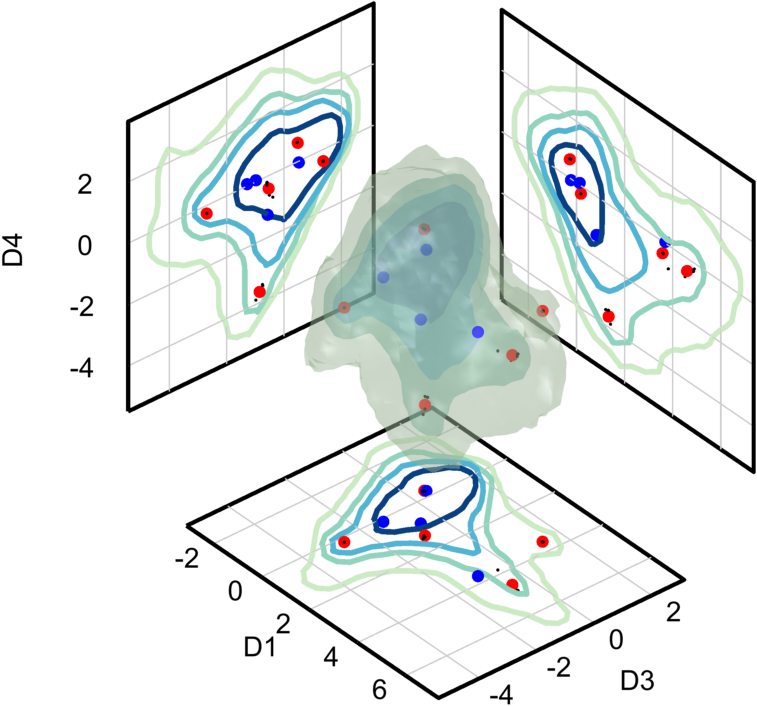

Data set description

The data used in this example are features representing the amount of damage in the nuclei used throughout this work. Using immunofluorescence techniques, the cells were stained so that DNA DSBs can be directly imaged. These images were then segmented and features extracted for each nuclei. The data set in this example has five features:

• The first feature is log(I_DSB/I_DAPI), where the fraction gives the fraction of DNA in a nucleus that has been damaged.
• The other four features are the first four principle components (PCA) of texture and granularity features from the DSB image channel

The images giving showing DSBs are not provided with the example data of this work.