Locating nuclei centers

Create helpers and visualize nuclei clumps

% Helper function for reading in mask images.
load_mask = @(n) imread(['exampleData\mask_' n '.tif']);

% Names of the trials - number corresponds to the normalized integrated
% brightness of the nuclei clump.
trials = {'2','3','4','5','67'};

% Show a random 9 nuclei clumps from the five test images.
visualizeNuclei();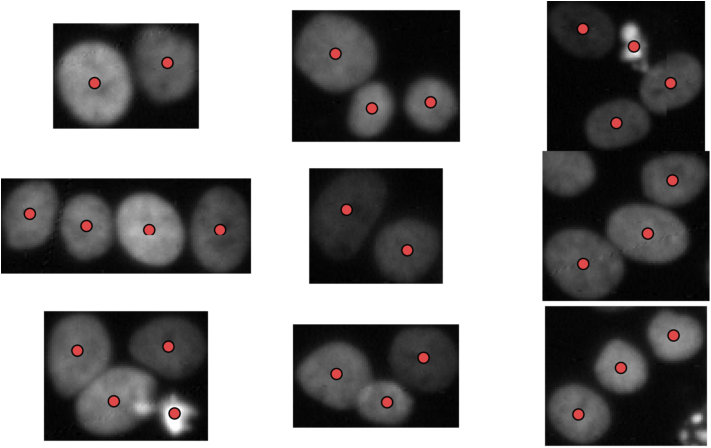

Setup SALR clustering parameters

The parameters needed to run SALR clustering can all be accessed and set using the class seedPointOptions. This class handles parameter validation as well as computing/visualizing the SALR particle interaction parameters/potential. Note, many of the values assigned below are the default values of seedPointOptions; they are only being assigned here for demostrative purposes.

options = seedPointOptions();

Set the particle initialization parameters.

• Use a uniform random point distribution. This will overlay a hexagonal lattice across the grid where the distance between two hexagon centers is 2*Wigner_Seitz_Radius. From each lattice cell, a point is then randomly selected from a set of possible initial positions r0set where the confining potential is less than Maximum_Initial_Potential.

options.Point_Selection_Method = 'r0set_uniformRandom';
options.Wigner_Seitz_Radius = 5;
options.Maximum_Initial_Potential = 1/5;

Set confining potential parameters.

• Use a confining potential based on the distance transform
• Scale the object so that its maximum distance transform value is 18. This gives SALR clustering a »scale invariance«.
• Add a small padding around the object to ensure the confining potential defined around the object.

options.Potential_Type = 'distance_transform';
options.Max_Distance_Transform = 18;
options.Potential_Padding_Size = 5;

Set the particle interaction parameter values.

• Note the Potential_Parameters are given in data units after scaling the data space so that the object has a maximum distance transform value of Max_Distance_Transform.

options.Potential_Parameters = [-1, 2, 13];

Set up replicates and minimum cluster size.

• Here we only use 1 replicate and accept all seed-points returned. We could get a small increase in performance by using several replicates and/or requiring a larger Minimum_Cluster_Size; however, when trying to locate nuclei centers, it is likely that we are trying to locate the centers of hundreds of thousands of nuclei. Therefore, increasing speed is may be more important that increasing performance by a small amount.

options.Iterations = 1;
options.Minimum_Cluster_Size = 1;

Set parameters controlling execution.

• Verbose will output information on the current iteration and the expected time of completion.
• Debug will return extra information.
• Use_Parallel will determine if the iterations are run in parallel.

options.Verbose = true;
options.Debug = false;
options.Use_Parallel = true;

Compute nuclei centers & visualize

The seed-points are simply computed by passing the binary mask and the seedPointOptions to computeNucleiCenters. computeNucleiCenters is essentially a wrapper for computeObjectSeedPoints that will automatically compute a set of possible initial positions based on the centers of curvature of each object boundary and then locate the seed-points of each object. Additionally, the output of the function contains the object number (nuclei clump) to which the seed-point belongs.

% Compute the results for each of the images.
for t = numel(trials):-1:1
    mask = logical(load_mask(trials{t}));
    nucleiCenters{t} = computeNucleiCenters(mask, options);
end

% Show a random 9 nuclei clumps from the five test images and show the
% computed nuclei centers.
visualizeNuclei(nucleiCenters);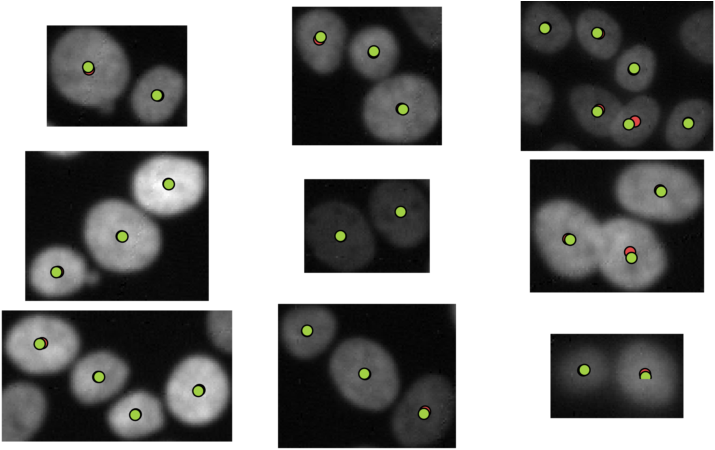

Evaluate performance

Here, lets test the performance of the SALR clustering results by computing the F1 score and the fractional distribution of the difference between the true number of nuclei in each clump and the computed number of nuclei in each clump.

• The F1 score depends on the distance at which we define a computed point to be a true positive point; thus, we can compute the F1 score at several such distances, from very close dr=3 to quite far dr=10.

% Initialize variables
dr = 3:10;
[F1, dN] = evaluatePerformance(nucleiCenters, dr);

% Plot the results
fig = figure('Units','inch');
fig.Position(3:4) = [4,6];

% F1 score
subplot(2,1,1)
line(dr, F1, 'Color', [223,73,73]/255, 'LineWidth', 3);
set(gca, 'XLim', [3,10], 'XTick', 3:10)
ylabel('F_1 Score')
xlabel('\delta r / pixels')

% FD_dN
subplot(2,1,2);
line(-3:3, dN, 'Marker', 'o', 'MarkerFaceColor', [223,73,73]/255, 'MarkerSize', 7, 'LineStyle', 'none', 'MarkerEdgeColor', 'none')
set(gca, 'XLim', [-3,3])
ylabel('FD_{dN}')
xlabel('dN')

setTheme(fig,'light')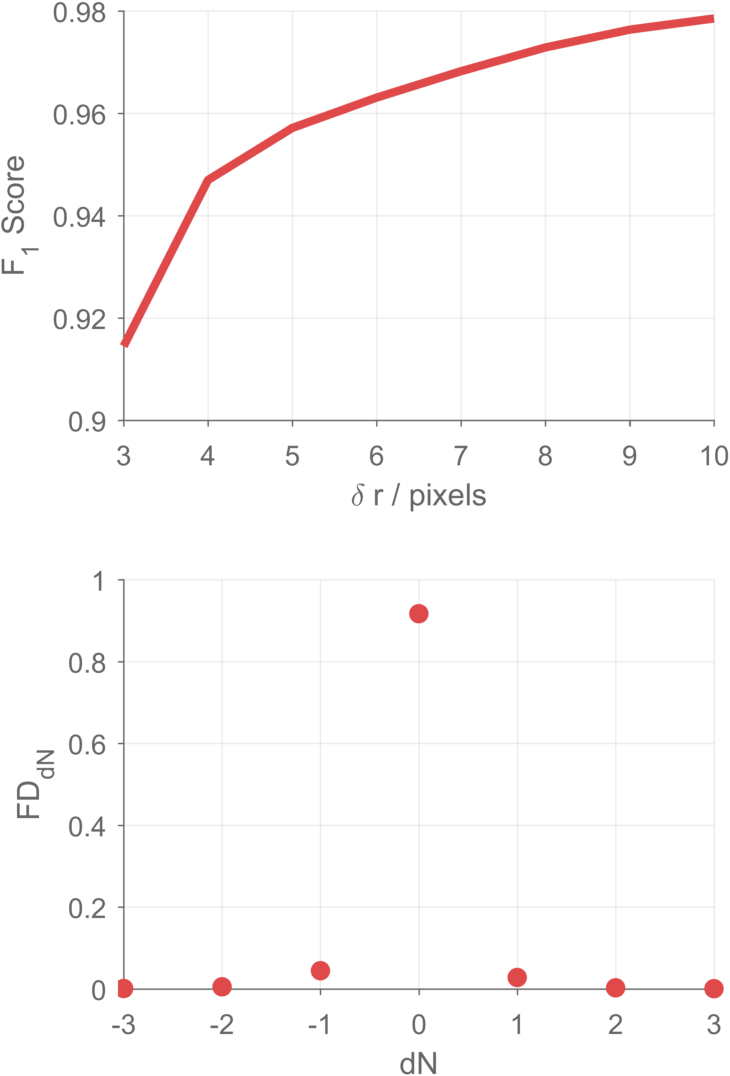

Data set description

The nuclei images used in this work were created as follows. A whole slide reader was used to image an entire coverslip full of cells. The nuclei were then segmented from the background using an adaptive Otsu thresholding¹ technique. The foreground regions were then analyzed and divided into five groups based on their normalized integrated DAPI florescence intensity. From each of these five groups, 484 objects were randomly selected and put into the images that are included in this work. For more information, please refer to our manuscript².