What can SALR clustering be used for?

Applications and validation

Locating object and distribution centers is a key step in both image processing and unsupervised machine learning. Both of these disciplines are used in the automated analysis of biological images. Here, SALR particle clustering is used to located the centers of overlapping cell nuclei as well as to locate clusters in scatter point data describing nuclei damage.

Table of Contents

Locating cell nuclei centers

When automatically analyzing a biological image it is necessary to separate the objects of interest (cells/nuclei) from the background; this is called »segmenting«. Some of the best methods of segmenting (repulsive level-set1 or active contours2) require »seed-points« before they can be used. A seed-point is a point known to be inside the object of interest. In order to obtain good segmentation results, it is important that there only be one seed-point per object located as close as possible to the object’s center.

Example of overlapping nuclei. Red points represent the manually labeled centers of the nuclei.

Results

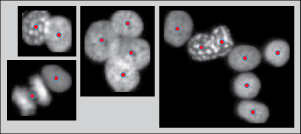
We applied SALR clustering to a set of ~2500 images of nuclei clumps (examples shown above) and compared the results with those of several of the leading and popular methods: MPV3, SPVQi1, SPVXu4, SBF5, gLoG6, MSER7, the distance transform local maximum. The comparison metric used is the F1 score, F1 = 2TP / (2TP + FN + FP), where TP, FN, and FP are the number of true positives, false negatives, and false positives.

The F1 score (F1=1: good, F1=0: bad) depends on how close a calculated seed-point must be to a true nuclei center before it is considered a TP point. For this reason, the F1 score is computed over a range, starting with the requirement that the seed-point and true center be very close to each other (δr=3 pixels), and going to the requirement that they need not be very close to each other (δr=10 pixels). Note, the average nuclei radius is 19 pixels.

The results of the comparison are in the figure above; SALR clustering is 8.2% better than the next best method at δr=3, and 3.0% better than the next best average F1 score (across δr).

Comparison of F1 versus δr. The truth data used in computing F1 was created by manually labeling the center of each nuclei in the images (~7800 nuclei).

Method

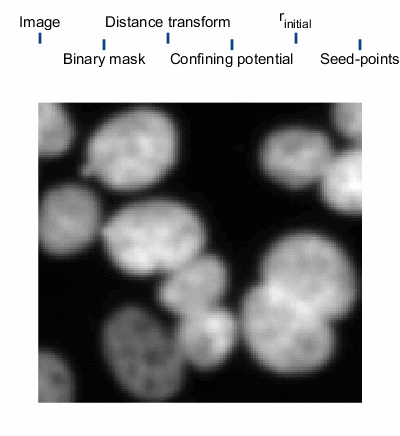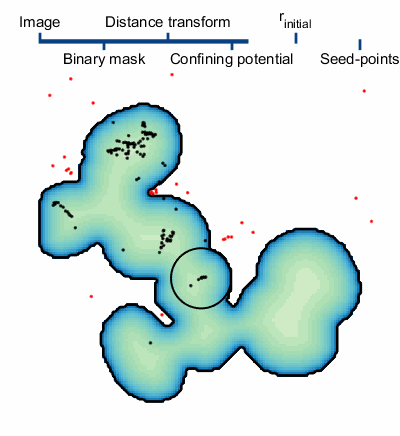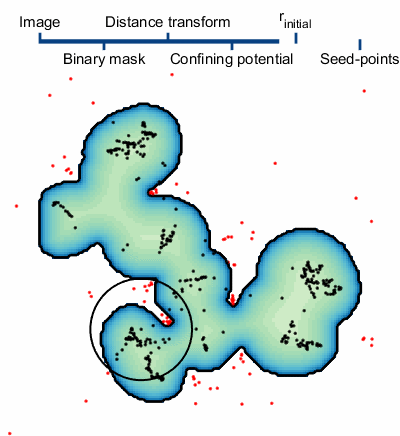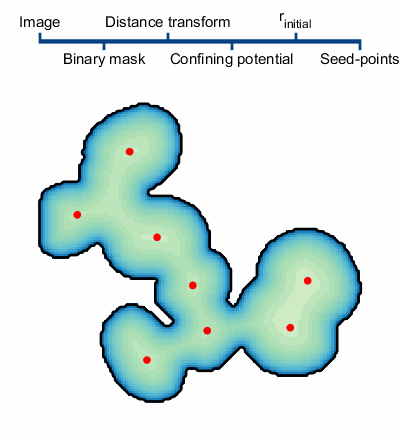
The steps of applying SALR clustering to locating the centers of cell nuclei are briefly described below and a graphical animation of the process can be seen to the right. For details, please see the manuscript8.

1. An initial segmentation of the image is made with the goal of creating a binary mask of the objects, but not trying to separate the overlapping objects.9

2. The confining potential is created using V(r)=1/dt(~BW(r)), where dt() is the distance transform and ~ represents the not operator. This confining potential can be improved to be scale invariant by first scaling the distance transform to a range of [1, λmax] before computing the confining potential.

3. The particles are initialized. There are two important quantities worth mentioning, the particle charge q and the particle’s initial positions. The charge is set to q=N-β, where N is the number of particle used in the simulation and β=1/3; this helps to normalize the interaction strength of large particle clusters. There are several methods of initializing the particle positions. The method we use first computes a set of possible positions using centers of curvature of each boundary vertex from the binary mask. We then overlay a hexagonal lattice over the binary mask and select one of the possible positions from each hexagon. The size of the hexagons, defined by the particles Wigner-Seitz radius rs, controls the number of particles in the simulation.

4. The particles dynamics are modeled and the centers of each cluster of particles are used as the final seed-points.

Data clustering

In unsupervised machine learning and data mining, data often comes in the form of scatter point data where each point is an observation and each dimension is a different measured quantity. The easiest way (but not the only way) to apply SALR clustering to scatter point data is to bin the data: we overlay a grid on the data and then count the number of points in each bin (grid element). The result of this can be thought of as a (multi-dimensional) image.

Example of binning 2D data.

Results

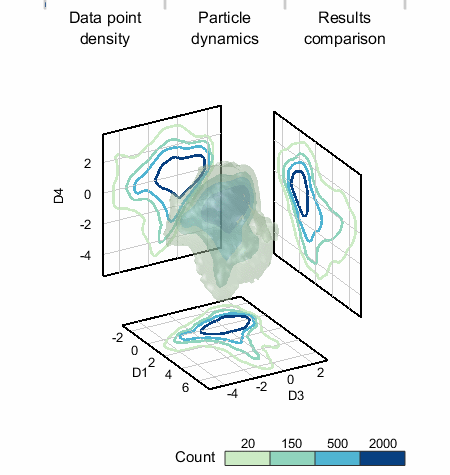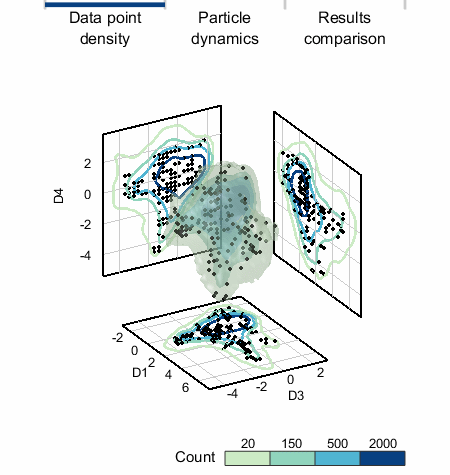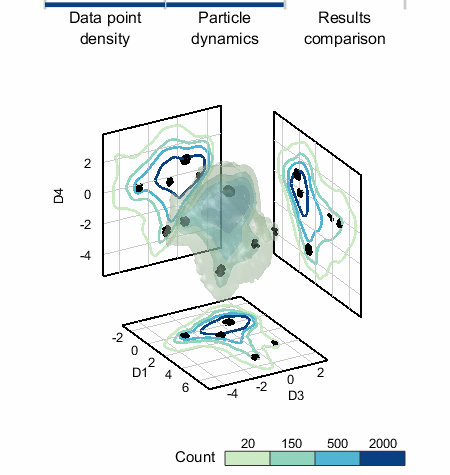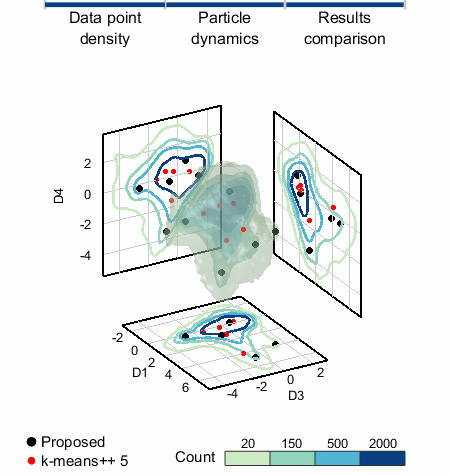
We applied SALR clustering to a 5D data set that represents healthy and damaged cells. To the left, the count isosurfaces of a projection of the data to 3D are shown. The data set has one dense region (which are the healthy cells) with three primary low density regions extending from it. K-means does not work well and produces cluster centers too biased towards the high density region, but »SALR clustering is able to locate all regions well.«

Method

The method of applying SALR clustering to scatter-point data is very similar to locating the center of nuclei above10, but there are a few differences.

  • The distance transform cannot be used to create the confining potential11; instead, one over the data density is used as the confining potential; however, it is very important that the magnitude of the potential gradient |∇V| is scaled so that it is approximately of the same order of magnitude as the particle repulsion 1/ra2.
  • The distance metric between the particles is changed to a Minkowski distance with an exponent of 4. This can be though of as requiring the particles to be close in all dimensions before they are attracted to each other.



  1. X. Qi, F. Xing, D. J. Foran, and L. Yang, IEEE Transactions on Biomedical Engineering 59, 754 (2012). ↩ ↩2

  2. X. Zhang, H. Su, L. Yang, and S. Zhang, Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 07-12-June, 5361 (2015). ↩

  3. B. Parvin, Q. Yang, J. Han, H. Chang, B. Rydberg, and M. H. Barcellos-Hoff, IEEE Transactions on Image Processing 16, 615 (2007). ↩

  4. H. Xu, C. Lu, and M. Mandal, IEEE Journal of Biomedical and Health Informatics 18, 1729 (2014). ↩

  5. P. Quelhas, M. Marcuzzo, A. M. Mendon¸ ca, and A. Campilho, IEEE Transactions on Medical Imaging 29, 1463 (2010). ↩

  6. H. Xu, C. Lu, R. Berendt, N. Jha, M. Mandal, and S. Member, Journal of Biomedical and Health Informatics XX, 1 (2016). ↩

  7. J. Matas, O. Chum, M. Urban, and T. Pajdla, In British Machine Vision Conference , 384 (2002). ↩

  8. J. Kapaldo, X. Han, and D. Mary, (submitted). ↩

  9. SALR clustering does not handle this step as it can be very different depending on the type of image. However, the binary mask used in creating the results were generated using an adaptive Otsu threshold12, and the manuscript8 shows that excellent results can also be obtained using the binary mask created by gLoG filtering followed by thresholding. ↩

  10. Abstractly, the problems are almost the same: locate the center of partially overlapping convex regions. ↩

  11. The distance transform will only work when the locally convex regions are about the same size in all directions. See Supplemental Note 3 of the manuscript8. ↩

  12. N. Otsu, IEEE transactions on systems, man, and cybernetics 9, 62 (1979). ↩